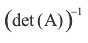ALGORITMO RC 666
Este es un algoritmo de cifrado simétrico desarrollado por nosotros
algoritmo RC666
Criptografía. FI. UNAM
martes, 6 de noviembre de 2012
martes, 9 de octubre de 2012
HOLA BIENVENIDOS A NUESTRO BLOG.
En este blog encontrarás los diferentes algoritmos criptográficos que se vieron hasta esta altura del semestre en la materia de Criptografía. Los cuales se automatizaron en diferentes lenguajes de programación: python, java y Dr. Racket.
Si estas interesado en ver su funcionamiento en este blog encontrarás los links para poder descargar los ejecutables , para que puedas hacer uso de ellos.
Ahora bien los algoritmos que encontrarás aquí son:
-ALGORITMO HILL
-ALGORITMO VERNAM
-ALGORITMO VIGENERE
-ALGORITMO AFÍN
-ALGORITMOS DE TRANSPOSICIÓN
La finalidad de este trabajo es para que tu como usuario puedas aprender sobre los algoritmos de cifrado que existen y conozcas la utilidad que pueden llegar a tener estos métodos, tanto en la actualidad como en el tiempo que se utilizaron.
Para su mejor comprensión daremos una explicación de lo que trata cada algoritmo de cifrado, que es lo que hace y como lo hace.
Los links de descarga para los programas, se encuentran AL FINAL de la explicación de cada algoritmo.
Esperamos tus comentarios y que verdaderamente disfrutes de este blog.
Sitio diseñado por:
- ALFARO DAMIAN JORGE ALEJANDRO
- AMÉZQUITA CANSECO JORGE
- REYES GÓMEZ DAVID ALEJANDRO
- VALVERDE DIEGO
ALGORITMO VERNAM
El cifrado de Vernam también llamado máscara desechable es parecido al cifrado de Vigenere solo que aquí la clave es aleatoria y tan larga como el mensaje, además se debe utilizar una sola vez. Claude Shannon en su trabajo “Teoría de las comunicaciones secretas” demostró que estas características hacen que este cifrado sea perfectamente seguro ya que no hay manera de criptoanalizarlo (es matemáticamente complicado).
Ejemplo:
Considerando los valores numéricos asignados a cada carácter del alfabeto castellano de la tabla de la figura 2.2.20, el cifrado de Vernam se realiza de la siguiente manera (figura 2.2.21):
Figura 2.2.20 Asignación de un valor numérico a cada carácter del alfabeto
Clave: EDSAS A CETNIEVED
MCla: BARRO Y CAÑABRAVA
Figura 2.2.21 Ejemplo del cifrado de Vernam(suma módulo 27)
Cripto: FDKRH Y EEHNJVVZD
Otra forma de realizar el cifrado de Vernam es realizando la suma módulo 2; para el ejemplo siguiente emplearemos el código ASCII (figura 2.2.22) para obtener el equivalente binario de cada carácter (figura 2.2.23)
Figura 2.2.22 Código ASCII
Ejemplo:
MCla: A LA ORILLA DE
Figura 2.2.23 Ejemplo del cifrado de Vernam (suma módulo 2)
DESCARGUE EL PROGRAMA VERNAM AQUI
ALGORITMO VIGENERE
Este cifrado consiste en realizar la suma (módulo el
número de caracteres en el alfabeto) de la clave y el texto en claro una vez
que se ha asignado un valor entero a cada carácter del alfabeto.
Ejemplo:
Figura
2.2.15 Asignación de un valor numérico a cada caracter del alfabeto
Clave: ERA
MCla: ENTONCES UNA ALDEA
Figura 2.2.16 Ejemplo del cifrado de
Vigenere
Cripto: IETSECIK UQR AOUEE
El MCla se recupera realizando la resta (módulo el
número de caracteres en el alfabeto) de la clave y el criptograma.
Otra manera de realizar el cifrado de un mensaje con
el método de Vigenere es la siguiente:
Se utiliza una clave y una matriz cuadrada que
contiene 26 alfabetos distribuidos tal y como muestra la figura 2.2.17.
Figura
2.2.17 Cuadrado de Tritemio
Ejemplo:
Clave: ERA
MCla: ENTONCES UNA ALDEA
El cifrado se realiza caracter por caracter, para ello
a cada caracter del mensaje en claro se le hace coincidir con un caracter de la
clave, si ésta es más corta que el mensaje en claro se repite las veces que sea
necesario (figura 2.2.18 a).
El primer renglón de la matriz corresponde a los
caracteres de la clave y la primera columna a los caracteres del mensaje en
claro (figura 2.2.18 b).
El criptograma es aquel carácter que resulte de la
intersección del renglón y la columna de donde se encuentren los caracteres de
la clave y el mensaje en claro respectivamente (figura 2.2.18 b).
Figura 2.2.18 Cifrado de Vigenere
utilizando el cuadrado de Tritemio
El mensaje en claro se recupera haciendo coincidir
cada caracter del criptograma con uno de la clave (figura 2.2.19 a) y buscando
en la columna de la letra de la clave el caracter del criptograma, la primera
letra que esté en el renglón de dicho caracter es la letra del mensaje en
claro, véase la figura 2.2.19 b:
Por ejemplo para buscar el MCla que corresponde al
criptograma obtenido en el ejercicio anterior:
Figura 2.2.19 Recuperación del
mensaje en claro del cifrado de Vigenere
lunes, 8 de octubre de 2012
ALGORITMO AFÍN
ALGORITMO AFÍN
El algoritmo de cifrado Afín es mono alfabético, simétrico y es por sustitución.
Un criptosistema afín es determinado por dos enteros a y b con las siguientes características:
- a ≥ 0
- b ≤ n
- n es el tamaño del alfabeto.
- Además a y n deben ser coprimos.
Para cifrar un mensaje con el algoritmo Afín, a cada caracter se le aplica la siguiente fórmula:
Ci = (a * Mi + b )mod n
Por ejemplo:
si a=3, b=5 y n=26
Y el mensaje a cifrar (Mi) es "hola"
Toda la aritmética debe ser realizada modulo n en este caso 26.
Las letras se numeran en orden alfabético de la siguiente forma:
Sustituyendo valores en la función para cifrar nuetra funcion queda:
Calculamos la sustitucion para cada caracter:
H =7 => C(7) = 7 * 3 + 5 = 26 mod 26 = 0 => A
O =14=> C(14) = 14 * 3 + 5 = 47 mod 26 = 21 => V
L =11 => C(11) = 11 * 3 + 5 = 38 mod 26 = 12 => M
A =0 => C(0) = 0 * 3 + 5 = 5 mod 26 = 5 => F
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
N
|
O
|
P
|
Q
|
R
|
S
|
T
|
U
|
V
|
W
|
X
|
Y
|
Z
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
Ci = (3 * Mi + 5 ) mod 26
H =7 => C(7) = 7 * 3 + 5 = 26 mod 26 = 0 => A
O =14=> C(14) = 14 * 3 + 5 = 47 mod 26 = 21 => V
L =11 => C(11) = 11 * 3 + 5 = 38 mod 26 = 12 => M
A =0 => C(0) = 0 * 3 + 5 = 5 mod 26 = 5 => F
El mensaje "hola" cifradoado es "AVMF"
Este es un sistema mono alfabético pues cualquier ocurrencia de un determinado caracter será reemplazado siempre por un único caracter en el mensaje cifrado ya que Ci = a Mi + b es una función.
El requerimiento de que a y n sean coprimos asegura que la función Ci = a Mi +b sea inyectiva ya que si la función no fuera inyectiva un cierto caracter en el mensaje cifrado podría corresponder a más de un caracter en el mensaje original y no podríamos descifrar el mensaje.
- NOTA:Dos números 'a' y 'b' son coprimos si su Máximo común divisor es 1. El concepto de números coprimos es de gran importancia en el mundo de la criptografía, este y otros conceptos de la teoría de números son utilizados muy a menudo para encriptar y desencriptar información.
En nuestro ejemplo 3 y 26 son coprimos mientras que 10 y 26 no lo son (MCD=2).
La función para descifrar es Mi = ( Ci − b )* a^−1 (mod n ) donde a^−1 es el inverso multiplicativo de a modulo n.
En el caso de a = 3 => a^−1 = 9 ya que 3 · 9 = 27 = 1 modulo 26, por lo tanto la función de descifrado será:
ALGORITMO HILL
Este sistema está basado en el álgebra
lineal y ha sido importante en la historia de la criptografía. Fue Inventado
por Lester S. Hill en 1929, y fue el primer sistema criptográfico polialfabético que era práctico para trabajar con más de tres símbolos simultáneamente.
Este sistema es polialfabético pues
puede darse que un mismo caracter en un mensaje a enviar se encripte en dos
caracteres distintos en el mensaje encriptado.
Suponiendo que trabajamos con un
alfabeto de 26 caracteres.
Las letras se numeran en orden
alfabético de forma tal que A=0, B=1, ... ,Z=25
Se elije un entero d que determina bloques
de d elementos que son tratados como un vector de d dimensiones.
Se elije de forma aleatoria una matriz
de d × d elementos los cuales serán la clave a utilizar.
Los elementos de la matriz de d × d
serán enteros entre 0 y 25, además la matriz M debe ser invertible en  .
.
 .
.
Para la encriptación, el texto es
dividido en bloques de d elementos los cuales se multiplican por la matriz d ×
d
Todas las operaciones aritméticas se
realizan en la forma modulo 26, es decir que 26=0, 27=1, 28=2 etc.
Dado un mensaje a encriptar debemos
tomar bloques del mensaje de "d" caracteres y aplicar:
M×Pi=C, donde C es el código
cifrado para el mensaje Pi
Ejemplo:
Para encriptar el mensaje "CODIGO" debemos encriptar los seis caracteres de "CODIGO" en bloques de 3 caracteres cada uno, el primer bloque
El primer bloque "COD" se
codificara como "WLP"
El segundo bloque "IGO" se
codificara como "GSE"
Luego 'CODIGO' encriptado equivale a
'WLPGSE'.
Observar que las dos "O" se codificaran
de forma diferente.
Para desencriptar el método es idéntico
al anterior pero usando la matriz inversa de la usada para encriptar.
Cálculo de la matriz inversa
Antes que nada debemos verificar que la
matriz elegida sea invertible en modulo 26. Hay una forma relativamente
sencilla de averiguar esto a través del cálculo del determinante. Si el
determinante de la matriz es 0 o tiene factores comunes con el módulo (en el
caso de 26 los factores son 2 y 13), entonces la matriz no puede utilizarse. Al
ser 2 uno de los factores de 26 muchas matrices no podrán utilizarse (no
servirán todas en las que su determinante sea 0, un múltiplo de 2 o un múltiplo
de 13)
Para ver si es invertible calculo el
determinante de A
5 (23 · 13 – 3 ·11) – 17 (9 · 13 – 3 · 2)
+ 20 (9 · 11 – 23 · 2) =
1215 – 1734 + 1060 = 503
503 = 9 mod 26
La matriz A es invertible en modulo 26
ya que 26 y 9 son coprimos
Donde CT es la matriz de cofactores de A
transpuesta
por lo tanto para el ejemplo la inversa
de 9 (mod 26) es 3 (mod 26) ya que
9 (mod 26) · 3 (mod 26) = 27 mod 26 = 1
(mod 26)
Por lo tanto 3 es la inversa
multiplicativa de 9 en modulo 26
Ahora aplicamos la formula de la inversa
Esta última es la matriz que utilizamos
para desencriptar
PROGRAMA HILL AQUI
sábado, 6 de octubre de 2012
ALGORITMOS DE TRANSPOSICION
Algoritmos de Transposición
A diferencia de los algoritmos de sustitución en donde los caracteres que conforman el mensaje en claro son sustituidos por otros, los algoritmos de transposición los cambian de posición dentro del mismo mensaje dando lugar al criptograma el cual no puede ser comprendido a simple vista.
TRANSPOSICIÓN SIMPLE
El procedimiento para realizar la transposición simple es el siguiente:
1. El mensaje en claro se reescribe en dos renglones: la primera letra en el primer renglón, la segunda en el segundo renglón, la tercera en el primer renglón, la cuarta en el segundo renglón y así uno y uno hasta acabar con todos los caracteres del mensaje en claro.
2. Se reescribe el mensaje por renglones.
La figura 2.2.25 muestra un ejemplo de transposición simple:
Figura 2.2.25 Ejemplo de transposición simple
Para recuperar el criptograma se realiza lo siguiente:
1. Se obtiene un número ´n´ de la siguiente manera: el número de caracteres que conforman el criptograma se divide entre dos, al resultado se le suma el residuo de la división.
2. Se toman los primeros n caracteres del criptograma y se colocan en el primer renglón, los restantes se colocan en un segundo renglón.
3. El mensaje en claro se conforma tomando uno y uno de los caracteres de cada renglón.
En la figura 2.2.26 se muestra la recuperación del MCla a partir del criptograma obtenido en el ejemplo de la figura 2.2.25.
Figura 2.2.26 Obtención del MCla de una transposición simple
Para realizar la transposición doble tenemos que llevar a cabo el mismo procedimiento dos veces arriba mencionado.
PARA DESCARGAR EL PROGRAMA DE TRANSPOSICIÓN, PULSE AQUI
Mas info sobre algoritmos de transposicion en este link
A diferencia de los algoritmos de sustitución en donde los caracteres que conforman el mensaje en claro son sustituidos por otros, los algoritmos de transposición los cambian de posición dentro del mismo mensaje dando lugar al criptograma el cual no puede ser comprendido a simple vista.
TRANSPOSICIÓN SIMPLE
El procedimiento para realizar la transposición simple es el siguiente:
1. El mensaje en claro se reescribe en dos renglones: la primera letra en el primer renglón, la segunda en el segundo renglón, la tercera en el primer renglón, la cuarta en el segundo renglón y así uno y uno hasta acabar con todos los caracteres del mensaje en claro.
2. Se reescribe el mensaje por renglones.
La figura 2.2.25 muestra un ejemplo de transposición simple:
Figura 2.2.25 Ejemplo de transposición simple
Para recuperar el criptograma se realiza lo siguiente:
1. Se obtiene un número ´n´ de la siguiente manera: el número de caracteres que conforman el criptograma se divide entre dos, al resultado se le suma el residuo de la división.
2. Se toman los primeros n caracteres del criptograma y se colocan en el primer renglón, los restantes se colocan en un segundo renglón.
3. El mensaje en claro se conforma tomando uno y uno de los caracteres de cada renglón.
En la figura 2.2.26 se muestra la recuperación del MCla a partir del criptograma obtenido en el ejemplo de la figura 2.2.25.
Figura 2.2.26 Obtención del MCla de una transposición simple
Para realizar la transposición doble tenemos que llevar a cabo el mismo procedimiento dos veces arriba mencionado.
PARA DESCARGAR EL PROGRAMA DE TRANSPOSICIÓN, PULSE AQUI
Mas info sobre algoritmos de transposicion en este link
Suscribirse a:
Comentarios (Atom)